• آموزش

بهینه­ سازی مهندسی و انواع روش های آن- بخش اول

بهینه سازی

تلاش برای دستیابی به بهترین نتیجه در مورد یک عملیات با در نظر گرفتن محدودیت­ها و شرایط مسئله، بهینه­ سازی نامیده می‌­شود.

به بیان دیگر بهینه­ سازی کمینه­ کردن یک کمیت غیرمطلوب، یا بیشینه­ کردن یک کمیت مطلوب بر مبنای محدودیت­‌ها و منابع در دست می‌باشد.

دسته­‌بندی­‌های متفاوتی برای مسائل بهینه­ سازی وجود دارد.

طراحی بهینه در یک نگاه استفاده موثر از منابع به منظور طراحی همه جانبه یک سیستم، جهت دستیابی به اهداف مورد نظر می­‌باشد، بدون آنکه به عملکرد مطلوب سیستم خدشه‌ای وارد گردد.

منظور از طراحی همه‌جانبه، طراحی است که در آن تمامی جنبه‌های اقتصادی- فنی در نظر گرفته شده و در عین حال کارایی مطلوب و مورد نظر سیستم از چشم طراح دور نمانده باشد.

بنابراین ممکن است طراحی یک سیستم برای یک کاربرد و شرایط معین بهینه باشد در حالی که آن طراحی برای همان سیستم در شرایط و کاربرد متفاوت دیگر بهینه نباشد.

براي شناخت يک پديده دو راه استفاده از تئوري‌­هاي علمي و انجام آزمايشات وجود دارد که راه جايگزين براي جبران کمبود تئوري­ هاي علمي، انجام آزمايش است.

بهینه­ سازی مهندسی به روش سطح پاسخ[1]

روش سطح پاسخ (RSM) در سال 1951، جهت بهبود فرآیندهای شیمیایی ارائه شد. هدف، بهینه‌سازی فرآیندهای شیمیایی و دستیابی به خروجی­‌هایی از قبیل بازده و خلوص بالاتر و هزینه‌ی پایین‌تر می­‌باشد.

همچنین متغیرها در فرآیندهای شیمیایی معمولاً دما، فشار و زمان فرآیند است.

روش سطح پاسخ مجموعه‌­ای از تکنیک­های آماری و ریاضی است که کاربرد آن برای مدلسازی و تحلیل مسائلی می‌باشد که یک پاسخ خروجی مورد نظر تحت تأثیر چندین متغیر مستقل دیگر قرار داشته و به مقدار بهینه­ برسد.

واژه‌ی سطح پاسخ نشان می‌دهد که تغییرات پاسخ در قبال متغیرهای کنترلی را باید مدنظر گرفت.

تعریف سطح پاسخ را می‌توان برای یک آزمایش با P فاکتور به صورت یک نمودار در فضای (P+1) بعدی نشان داد. به عنوان مثال در شکل زیر یک نمونه با دو متغیر مستقل x₁ و x₂ و متغیر وابسته y (پاسخ) که تابعی از x₁ و x₂ است، نمایش داده شده است.

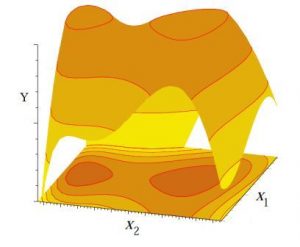
روش سطح پاسخ نقاط نمونه را در فضای متغیرهای ورودی تصادفی طوری قرار می‌دهد که تابع مناسب تقریبی برای آن یافت شود. اساساً این تابع یک تابع چند جمله‌ای درجه‌ي دوم است.

در این رابطه تابع تخمینی به صورت رابطه زیر تعیین می‌شود.

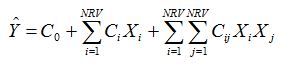
که در رابطه فوق C₀ ضریب ثابت، C_i ضرایب ترم‌های خطی و C_ij ضرایب ترم‌های درجه دوم است.

ویژگی­ های روش سطح پاسخ

روش سطح پاسخ یک روش ابتکاری در بهینه­ سازی مهندسی است که پس از تخمین روابط رگرسیونی^[2] بین متغیرهای قابل کنترل و متغیر پاسخ، سعی در تعیین مقداری از متغیرهای کنترلی دارد، که بهترین مقدار پاسخ را دربرداشته باشند.

فرآیند بهینه‌سازی توسط RSM را می‌توان به سه مرحله تفکیک کرد. مرحله نخست، مشخص نمودن پارامترهای مستقل و سطوح آن‌ها می‌باشد.

مرحله دوم، گزینش طرح آزمایشی و پیش بینی و ارزیا­بی رابطه مدل نهایی، بدست آوردن و رسم نمودار روش پاسخ به عنوان تابعی از پارامترهای مستقل و تعیین نقاط بهینه است.

در گام­‌های روش سطح پاسخ، از مدل‌های رگرسیونی چندجمله‌ای خطی (درجه اول) و درجه دوم استفاده می‌شود. همچنین در روش سطح پاسخ مقادیر باقیمانده در مدل‌های رگرسیون دارای میانگین صفر و واریانس ثابت در فضای آزمایش‌­ها هستند.

در مرحله بعد بایستی جهت مطلوب برای تغییرات متغیرهای ورودی تعیین شود تا در گام بعدی به بهینه ­سازی متغیر پاسخ پرداخته شود. روش سطح پاسخ از بردار گرادیان مربوط به سطح پاسخ، برای تعیین جهت بهینه­ سازی بهره می‌­برد.

در واقع این مرحله، تکنیک­‌های ریاضی (نه آماری) به منظور بیشترین کاهش یا افزایش در تابع هدف (سطح پاسخ) به کار گرفته می‌شود.

در مرحله‌ی پایانی با استفاده از مشتق‌گیری، روش سطح پاسخ به کشف نقطه بهینه در چند جمله‌ای درجه دوم می‌پردازد. همچنین می‌توان با استفاده از تحلیل‌های ریاضی نقطه بهینه به لحاظ محلی، مطلق یا زینی بودن را مشخص نمود.

به منظور بهینه­ سازی به روش سطح پاسخ از دو روش طراحی آزمایش مرکب مرکزی (CCD) و ماتریس باکس-بِنکن (BBM) استفاده می‌شود.

روش طراحی آزمایش مرکب مرکزی متشکل از نقاط مرکزی، محوری و گوشه‌های یک مکعب است. در طراحی آزمایش به روش BBM نقاط طراحی شامل نقاط مرکزی و نقاط میانی یک مکعب می‌باشد.

موقعیت نقاط نمونه برای یک مسئله با سه متغیر ورودی تصادفی مطابق شکل 2 می‌باشد.

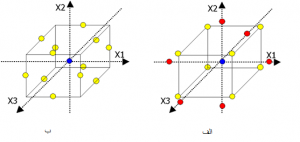
روش سطح پاسخ در مقایسه با روش‌های کلاسیک آماری یا روش­های بهینه­ سازی که یک متغیره می‌باشند، مزایای متعددی دارد. مزیت اصلی آن است که با تعداد آزمایش کم، اطلاعات زیادی ارائه می‌دهد.

در حقیقت روش‌­های کلاسیک زمان‌بر بوده و به تعداد زیادی آزمایش برای بیان رفتار سیستم نیازمند می­‌باشند. ثانیا در RSM می­توان اثر برهم کنش بین پارامترهای مستقل بر پاسخ را بررسی کرد.

به ویژه در مواقعی که در سیستم، اختلاف یا ناسازگاری داشته باشیم، از RSM می‌توان به خوبی بهره گرفت.

از محدودیت‌های این روش می‌توان به احتمال گمراه کنندگی تغییرات بزرگ در فاکتورها و نیز عدم تعریف درست فاکتورهای بحرانی در بعضی موارد، اشاره نمود.

از اینکه تا انتهای این مقاله همراه ما بودید بسیار سپاسگزاریم.

[1] Response Surface Method (RSM)

[2] Regression

خدمات و منتورینگ بنوموسی

شرکت بنوموسی با ارائه جلسات منتورینگ آباکوس راهنمای شما عزیزان در جهت رفع و بهبود ایرادات فنی و مهندسی پروژه های صنعتی و دانشجوی تان در زمینه مدل‌سازی، تحلیل، و صحت‌سنجی نتایج می باشد. این جلسات به صورت آنلاین و حضوری برگزار می‌شود و نیم ساعت اول رایگان است. برای اطلاعات بیشتر و رزرو وقت، از صفحه منتورینگ اباکوس ما دیدن کنید.

برای استفاده از خدمات شبیه‌سازی و مشاوره رایگان ما، کافی است با ما تماس بگیرید. ما در تمام مراحل پروژه کنار شما هستیم تا بهترین نتایج را به‌دست آورید.

برای کسب اطلاعات بیشتر و دریافت منتورینگ ، لطفاً با ما تماس بگیرید یا از وب‌سایت Banumusagr بازدید کنید. تیم ما آماده است تا شما را در دستیابی به نتایج مطلوب در تحلیل‌های عددی و شبیه‌سازی‌های مهندسی یاری کند.

راه های ارتباطی با شرکت بنوموسی :

TELEGRAM : https://t.me/BanuMusaGr

ایمیل: info@BanuMusaGr.com

تلفن همراه:  388 20 55 0915

تلفن:  35424520– 51 (98+)

آدرس: مشهد – کیلومتر 12 بزرگراه آسیایی (جاده قوچان)- جاده شهرک صنعتی توس- شهرک فناوری صنایع غذایی و بیوتکنولوژی شمال شرق- معاونت صنایع کوچک- مرکز خدمات.