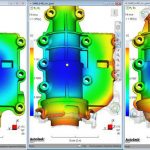
حلگر صریح و ضمنی پرکابرد در نرم افزارهای اجزا محدود FEM | مقایسه ی 2 حلگر صریح و ضمنی در آباکوس
آخرین بروزرسانی 1401.08.09
دو حلگر پرکابرد در نرم افزارهای اجزا محدود FEM
امروزه اکثر مهندسان از دو حلگر پرکاربرد در نرم افزارهای اجزا محدود (FEM) برای حل و تحلیل مسائل کاری و تحقیقاتی خود استفاده میکنند. در این نرم افزارها از روشهای مختلف عددی برای انتگرالگیری و حل معادلاتدیفرانسیل معمولی و PDE بهره گرفته میشود. روشهای عددی که برای انتگرالگیری در دامنه زمان مورد استفاده قرار میگیرند، معروف به دو حلگر صریح و ضمنی میباشند.
برای مطالعه در مورد FEM میتوانید به این سایت مراجعه کنید
روش حلگر ضمنی در نرم افزار های اجزا محدود (FEM)
روش ضمنی (Implicit) معادلهی دیفرانسیل را به مجموعهای از معادلات خطی وابسته به مجهولات تقسیم و به صورت همزمان حل میکند. گرچه روند این کار خطی است.
اما در صورتی که دامنه زمان به فاصلههای کوچکی از هم تقسیم شود، میتواند مسائل غیر خطی را هم حل کند. اگر این فاصلههای زمانی به اندازه کافی کوچک باشند، حل مسالهی غیرخطی میتواند همگرا شود.
در این روش برخلاف روش صریح با استفاده از اطلاعات موجود نمیتوان حالت سیستم را محاسبه کرد بلکه باید مجموعه معادلاتی حل شود تا به پاسخ موردنظر دست پیدا کنیم. برای حل این معادلات نیاز به یک الگوریتم غیرخطی داریم که از روش نیوتن استفاده میشود.
نکته: حلگر ضمنی هم در حل مسائل استاتیکی کاربرد دارد و هم دینامیکی (با سرعت پایین، یعنی اگر هم نیرو دینامیکی داریم باید به آرامی اعمال شود تا حاصل ضرب جرم در شتاب قابل چشم پوشی باشد).
گفتنی است یکی از مزایای روش ضمنی این است که نتایج نسبت به روش صریح دقیق تر بوده و به واقعیت نزدیکتر است.
واضح است که در حل ضمنی حجم محاسبات در یک بازه زمانی بسیار بیشتر از حل صریح است؛ چرا که باید مجموعهای از معادلات حل شود و برای تحلیلهای غیر خطی ممکن است چندین بار تکرار شود و زمان بیشتری میگیرد.
در این روش برخلاف روش صریح محدودیتی برای بزرگ کردن بازه زمانی وجود ندارد؛ چون روش محاسبات به شیوه نیوتن انجام میشود و از طریق اصلاح و تکرار جواب حاصل میشود. پس بزرگ در نظر گرفتن بازه زمانی مشکلی ایجاد نمیکند.
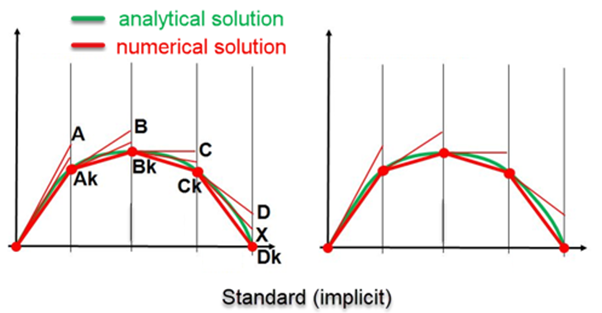
شکل زیر نحوه محاسبه شیب خط در حل استاندارد یا ضمنی نشان داده شده است. همانطور که از شکل مشخص است اندازه گام زمانی تاثیر در دقت نتایج ندارد.
نمونه پروژههای مرتبط را ببینید
روش حلگر صریح در تحلیل اجزا محدود
حلگر صریح (explicit) از روشهای پیشرو برای حل تمام مجهولات در هر گام زمانی به صورت تکراری استفاده میکند.
نقطهی قوت روش ضمنی حل معادلات دیفرانسیل در حوزههای مختلف مثل استاتیک، حالت پایدار، دامنه فرکانسی و مسائل گذرای دامنه زمان میباشد.
در مقابل، روش صریح، تنها میتواند برای حل مسائل گذرا استفاده شود. با این وجود این روش یک ویژگی منحصربهفرد دارد و آن این است که بسیار پایدار است و قادر است مسائل غیرخطی را بخوبی حل کند.
هر دو روش ضمنی و صریح میتوانند برای روشهای عددی اجزا محدود(FE)، المان مرزی (BE)، هیدرودینامیک ذرات روان (SPH) و روش المان آزاد گالرکین (EFG) مورد استفاده قرار گیرند.
با وجود آنکه تمام این روشها میتوانند برای حل مسائل غیرخطی مورد استفاده قرار گیرند، تفاوتها در راندمان عددی، پایداری حل و دقت از مسائل مهم در انتخاب هر یک از این روشها در تحلیلهای مختلف میباشد.
در روش حل صریح با استفاده از برونیابی حالت سیستم در نقطه بعد با استفاده از اطلاعات نقطه کنونی بدست میآید. در این روش محاسبات سختی زیادی ندارد چون اطلاعات مورد نیاز موجود است و به همین دلیل سرعت محاسبات بالاست.
در حلگر صریح نمیشود طول بازههای زمانی را افزایش داد چون از روش برونیابی استفاده میشود و این روش از دادههایی استفاده میکند که خارج از بازهای است که درباره آن اطلاعات داریم.
پس حتما خطا در حل صریح بیشتر میشود و این خطاها در بازههای زمانی با هم جمع شده و در نهایت تمام حل دچار خطا میشود.
البته نرم افزارهای اجزامحدود مثل آباکوس، انسیس و LS-Dyna بزرگترین گام زمانی که حل را دچار خطا نکند محاسبه میکند.
نکته: حلگر صریح فقط در تحلیل مسائل دینامیکی کاربرد دارد. به عنوان مثال پدیدههای دینامیکی با سرعت بالا مثل نیروهای انفجاری یا ضربهای یا مسائلی با برخوردهای پیچیده و همینطور مسائلی که در آن شکست یا خرابی مواد در آن مطرح است و…
شکل زیر به صورت شماتیک نحوه محاسبه شیب خط با استفاده از روش صریح نشان داده شده است. همانطور که از شکل مشخص است با کاهش گام زمانی پایدار نتایج به نتایج تحلیلی نزدیکتر میشود.
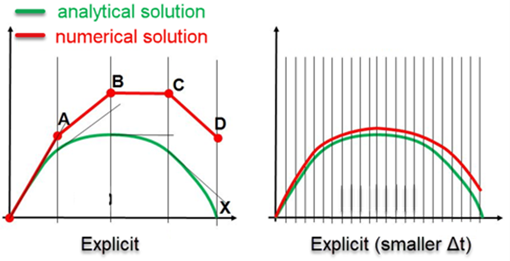
پایداری در روش صریح
پیشتر گفتیم که در روش صریح طول بازههای زمانی کوچک است تا دچار خطا نشود. البته این پایداری بازه زمانی به طور مشروط پایدار است،که حد پایداری در دو حالت (وجود و عدم وجود دمپینگ)به صورت زیر است:
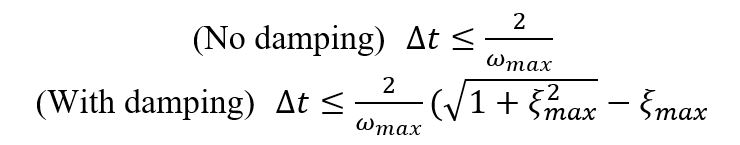
برخلاف شواهد مهندسی، وارد کردن میرایی به حل، گام زمان پایدار (Stable Time Increment) را کاهش میدهد. در حل صریح مقدار کمی میرایی به شکل ویسکوزیته حجیم برای کنترل نوسانات فرکانس بالا وارد میشود.
میتوان با استفاده از فرمول بالا گام زمانی را تخمین زد. که در این فرمول L طول کوچکترین المان و C سرعت موج تنش است.
نکته: فرمول بالا برای المانهای میلهای استفاده میشود. برای المانهای سهبعدی و دوبعدی از فرمول زیر استفاده برای محاسبه دقیقتر میتوان استفاده کرد.
تجربه نشان داده است برای تخمین اولیه فرمول بالا بسیار کارآمد است. لازم به ذکر است در نرم افزار های اجزا محدود اکثرا گام زمان پایدار در ابتدای تحلیل به کاربر نشان داده میشود.
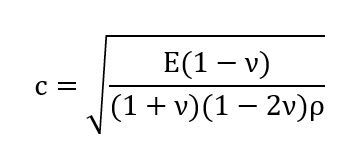
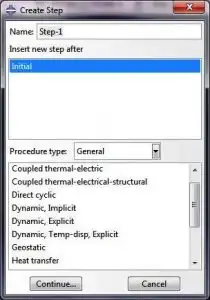
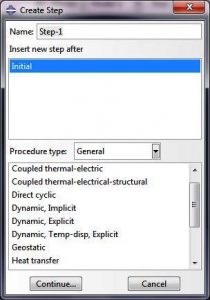
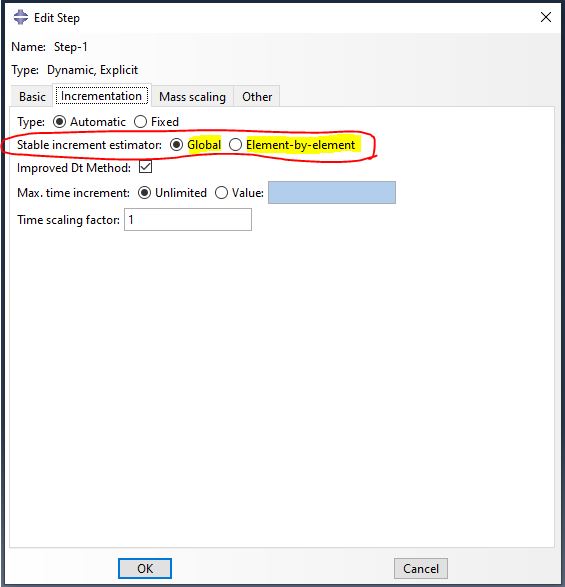
نکته: در نرم افزار آباکوس، 2 راه برای تخمین حد پایداری وجود دارد (شکل زیر)؛ المان به المان (Element-by-Element) و گلوبال (Global) که در ماژول Step قابل تنظیم است.
روش المان به المان برای تحلیل های دمایی و مکانیکی و روش گلوبال برای تحلیل های مکانیکی استفاده می شود. تخمین المان به المان براساس کوچکترین اندازه گام زمانی در هر المان برای تحلیلهای مکانیکی و حرارتی عمل میکند. این روش محافظهکارانه است و اندازه گام زمانی آن از حد پایداری واقعی کوچکتر است. حد پایداری واقعی براساس ماکزیمم فرکانس کل مدل محاسبه میشود. به طور کلی، قیودی مثل شرایط مرزی و تماسهای سینماتیک بر فشرده شدن طیف مقدار ویژه (eigenvalue spectrum) تاثیر میگذارد و تخمین حد پایداری به روش المان به المان این موضوع را مدنظر قرار نمیدهد.
برخی از مشخصات حلگر صریح و ضمنی در نرم افزارهای FEM بهصورت زیر است:
تا اینجا تا حد امکان خلاصهای از هر دو حلگر ارائه شد. اما نکتههای زیر برای اینکه چه حلگری را برای تحلیل تان استفاده کنید، میتواند مفید باشد.
با افزایش اندازهی مسئله هزینهی تحلیل در حلگر صریح بهصورت خطی افزایش مییابد، اما درروش ضمنی بهصورت نمایی یا حداقل با شیب بزرگتری نسبت به حلگر صریح افزایش مییابد. به همین دلیل هر چه اندازهی سازه و مدل بزرگ میشود، استفاده از روش صریح مقرونبهصرفهتر است. برای حل مسائل دارای ناپیوستگی، روش انتگرالگیری صریح بهتر از روش ضمنی است.
برای مسائلی که در آن انتشار تنش اهمیت دارد، حل صریح از نظر زمان حل بهصرفهتر است.
در مسائل با تغییر شکل و چرخش بزرگ، مسائل دینامیکی با سرعت بالا، مسائل واماندگی و یا نرم شدگی در مواد و مسائل غیرخطی میتوان از حل صریح استفاده کرد.
هرچند گامهای زمانی در روش صریح کوچکتر از روش ضمنی است، اما به دلیل عدم نیاز به الگوریتم حل معادلات ماتریسی (تشکیل ماتریس جرم و سفتی و معکوس سازی آنها)، هزینهی محاسبات بسیار کمتر از روش ضمنی است؛ بنابراین با افزایش تعداد درجات آزادی این روش مقرونبهصرفه تر است.
اندازهی گام زمانی در حل صریح محدود و بهصورت مشروط پایدار است درحالیکه در حلگر ضمنی شرط پایداری وجود ندارد و تنها دقت و صحت جواب گام زمانی را کنترل میکند. به بزرگترین گام زمانی پایدار اصطلاحا گام زمانی کورانت (Courant time step) گفته میشود. زمان کورانت به معنی مقدار زمان لازم برای عبور موج با سرعت صوت از یک المان است.
روش صریح نامهای دیگری مثل روش باز (Open) و روش پیشگو (Predictor) دارد و روش ضمنی بانامهایی چون بسته (Closed) و اصلاحگر (Corrector) هم شناخته میشود.
در روش صریح بهتر است بازههای زمانی حل کوچک باشد تا بتواند روند حرکت موج را دنبال کند. زیرا اگر سرعت حرکت موج از سرعت حلگر بیشتر شود جوابهای درستی حاصل نمیشود. این مشکل بیشتر در المانهای کوچک رخ میدهد. مثلا موج تنش به سرعت از المان میگذرد و باید برای برطرف کردن این مشکل بازه زمانی براساس کوچکترین المان بدست آید. پس میتوان فهمید که مشبندی درست در روش صریح تاثیر زیادی بر درستی آنالیز دارد.
در حل صریح مجموع تمام نیروها باید با ضرب شتاب در جرم برابر باشد (قانون دوم نیوتن).
Sum of all forces = mass x acceleration
اگر میزان سرعت/ نرخ کرنش بیشتر از 10متر ثانیه یا 10 واحد بر ثانیه باشد بهتر است از روش صریح استفاده شود.
کمی تخصصی تر!
در حل صریح هدف محاسبه شتاب است. در بیشتر موارد، ماتریس جرم lumped و قطری در نظر گرفته میشود. معکوس کردن یک ماتریس قطری راحتتر است (پیشنهاد میشود به کتابهای ریاضیات پیشرفته مهندسی مراجعه شود).
همچنین شتاب در گام nام ، سرعت در گام n+1/2 و جابهجایی در گام n+1 محاسبه میشوند.
انتخاب سابروتین با توجه به نوع حلگر در آباکوس
در نرمافزار اجزا محدود Abaqus برای حل مسائل غیرخطی امکان استفاده از هر دو نوع حلگر صریح و ضمنی وجود دارد. همچنین برای سابروتین نویسی تقریبا برای هر حلگر یک سابروتین درنظر گرفته شده است که بسیار مفید است. مثلا برای سابروتیننویسی رفتار ماده در این نرم افزار امکان استفاده از دو زیربرنامهی UMAT و VUMAT وجود دارد.
در این زیربرنامه ها معادلات متشکله و سازگاری ماده تعریف می گردند. زیربرنامهی UMAT برای حل ضمنی و زیربرنامهی VUMAT برای حل صریح مورد استفاده قرار میگیرد. در زیربرنامهی VUMAT از روش پیش رو- پس رو اویلر جهت محاسبات عددی استفاده میشود.
همانطور که اشاره شد این زیربرنامه، به تعداد تکرارهای کمتری برای رسیدن به جواب احتیاج دارد.
از طرفی نیازی به تعریف ماتریس ژاکوبی ندارد؛ البته لازم است برای آن حد پایداری کورانت-فردریش- لوی تعریف گردد. این حد پایداری محدودهی گام زمانی را مشخص میکند که معرف زمان لازم برای انتشار موج است. مقدار گام زمانی باید کمتر از حد پایداری باشد.
هنگام استفاده از زیر برنامهی VUMAT مقدار گام زمانی باید بهصورت دستی در ماژول step تعریف شود.
عدم تعریف مقدار مناسب برای گام زمانی موجب ناپایداری عددی در حل صریح میشود. هنگامی که جوابها ناپایدار میشوند، پاسخ زمانی متغیرهای حل، مثل جابهجایی، شتاب و … نوسانات زیادی خواهند داشت؛ در این حالت انرژی تعادل (Energy Balance) نیز بهشدت تغییر میکند.
اگر مدل فقط شامل یک نوع ماده باشد، گام زمانی اولیه فقط بهاندازهی کوچکترین المان بستگی دارد.
اما اگر مدل شامل چند نوع ماده باشد ولی اندازهی المانها برابر باشد، مادهای که دارای بیشترین سرعت موج است گام زمانی اولیه را تعیین میکند. در مسائل غیرخطی، فرکانس مدل دائماً تغییر میکند، بنابراین حد پایداری نیز تغییر میکند.
همانطور که ذکر شد هر حلگر مزایا و معایبی دارد که تحلیلگر باید با استفاده از تجربه و متناسب با مساله بهترین و مناسبترین حلگر را انتخاب کند.
امیدوارم این مطلب مفید بوده باشه. در انتها اگر سوال و نظری در مورد این موضوع دارید میتوانید در قسمت نظرات ثبت کنید. در اولین فرصت پاسخ خواهم داد.
خدمات و منتورینگ بنوموسی
شرکت بنوموسی با ارائه جلسات منتورینگ آباکوس راهنمای شما عزیزان در جهت رفع و بهبود ایرادات فنی و مهندسی پروژه های صنعتی و دانشجوی تان در زمینه مدلسازی، تحلیل، و صحتسنجی نتایج می باشد. این جلسات به صورت آنلاین و حضوری برگزار میشود و نیم ساعت اول رایگان است. برای اطلاعات بیشتر و رزرو وقت، از صفحه منتورینگ اباکوس ما دیدن کنید.
برای استفاده از خدمات شبیهسازی و مشاوره رایگان ما، کافی است با ما تماس بگیرید. ما در تمام مراحل پروژه کنار شما هستیم تا بهترین نتایج را بهدست آورید.
برای کسب اطلاعات بیشتر و دریافت منتورینگ ، لطفاً با ما تماس بگیرید یا از وبسایت Banumusagr بازدید کنید. تیم ما آماده است تا شما را در دستیابی به نتایج مطلوب در تحلیلهای عددی و شبیهسازیهای مهندسی یاری کند.
راه های ارتباطی با شرکت بنوموسی :
TELEGRAM : https://t.me/BanuMusaGr
ایمیل: info@BanuMusaGr.com
تلفن همراه: 388 20 55 0915
تلفن: 35424520– 51 (98+)
آدرس: مشهد – کیلومتر 12 بزرگراه آسیایی (جاده قوچان)- جاده شهرک صنعتی توس- شهرک فناوری صنایع غذایی و بیوتکنولوژی شمال شرق- معاونت صنایع کوچک- مرکز خدمات.
حلگر صریح چیست و چه کاربردی دارد؟
حلگر صریح (Explicit) از روشهای پیشرو برای حل معادلات دیفرانسیل در مسائل گذرا استفاده میکند. این حلگر مناسب تحلیلهای دینامیکی با سرعت بالا، مانند برخوردها و انفجارها است و به دلیل سرعت بالا، برای مسائل بزرگ مقیاس بسیار کارآمد است.
تفاوت اصلی بین حلگر صریح و ضمنی چیست؟
حلگر صریح از روش برونیابی استفاده میکند و برای مسائل دینامیکی با سرعت بالا مناسب است، در حالی که حلگر ضمنی (Implicit) برای مسائل استاتیکی و دینامیکی با سرعت پایین بهتر است و نتایج دقیقتری ارائه میدهد، هرچند زمان محاسبات آن بیشتر است.
در چه مواقعی باید از حلگر ضمنی استفاده کنیم؟
حلگر ضمنی برای تحلیل مسائل پایدار استاتیکی و دینامیکی، به ویژه در مسائل غیرخطی که نیاز به دقت بالا دارند، مناسب است. همچنین در مسائلی که بازه زمانی بزرگتر است، استفاده از این حلگر مقرونبهصرفهتر است.
آیا حلگر صریح برای همه مسائل مناسب است؟
حلگر صریح بیشتر برای مسائل دینامیکی با سرعت بالا و برخوردهای پیچیده کاربرد دارد. اگر مسئله شامل تغییر شکلهای بزرگ یا خرابی مواد باشد، حلگر صریح بهترین گزینه است. اما در مسائل استاتیکی یا دینامیکی با سرعت پایین، بهتر است از حلگر ضمنی استفاده شود.
چطور میتوانم مشبندی مناسبی برای حلگر صریح انتخاب کنم؟
رای جلوگیری از ناپایداری در حلگر صریح، مشبندی باید بر اساس کوچکترین المانهای مدل انجام شود. همچنین، گام زمانی باید به اندازه کافی کوچک باشد تا نوسانات ناخواسته در نتایج ایجاد نشود.
آیا حلگر صریح برای مسائل غیرخطی مناسب است؟
بله، حلگر صریح در حل مسائل غیرخطی، بهویژه مسائل برخوردی و خرابیهای مواد، بسیار پایدار و کارآمد است.
چطور میتوانم از خدمات مشاوره و منتورینگ استفاده کنم؟
برای دریافت مشاوره و منتورینگ در زمینه انتخاب حلگر مناسب و تحلیل مسائل پیچیده FEM، میتوانید از طریق لینکهای موجود در سایت جلسات را رزرو کنید.
مشکلات رایج هنگام استفاده از حلگرهای صریح و ضمنی چیست؟
یکی از مشکلات رایج در حلگر صریح ناپایداری عددی در صورت انتخاب گام زمانی نادرست است. همچنین، در حلگر ضمنی زمان محاسبات بسیار طولانی میشود، بهویژه در مسائل غیرخطی.