سیستم مختصات تحلیل اجزا محدود (FEA)

• آموزش, بلاگ

سیستم مختصات تحلیل اجزا محدود (FEA) ، برای اینکه بتوانیم مدل‌ها را دقیق شبیه‌سازی کنیم و نیروها، تغییر شکل‌ها، و شرایط مرزی را درست تعریف کنیم، از چند نوع سیستم مختصات تحلیل اجزا محدود استفاده می‌کنیم. این سیستم‌های مختصات کمک می‌کنند که موقعیت‌ها، جهت‌ها، و حرکات را به درستی در فضای سه‌بعدی تعریف کنیم. سه نوع اصلی سیستم مختصات تحلیل اجزا محدود که در این زمینه کاربرد دارند.

انواع سیستم مختصات تحلیل اجزا محدود

سیستم مختصات دکارتی (Cartesian Coordinate System) :
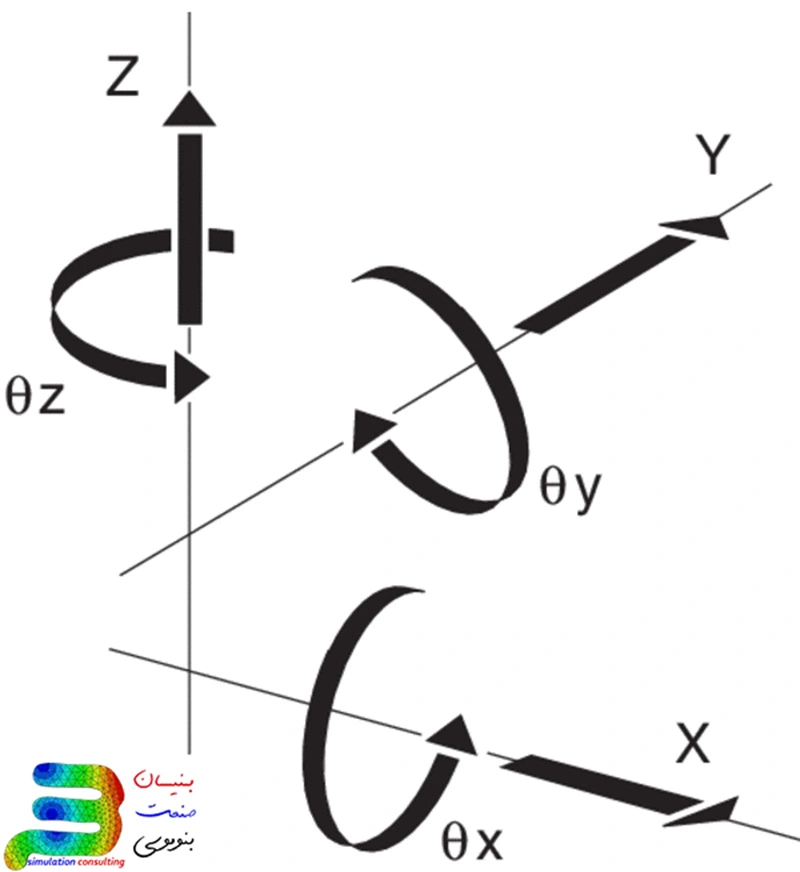
این همان سیستمی است که ما در مدرسه‌ها یاد گرفتیم.در این سیستم مختصات تحلیل اجزا محدود سه محور X، Y، و Z داریم که همدیگر را در زاویه ۹۰ درجه قطع می‌کنند. این سیستم به دلیل سادگی و کاربرد گسترده‌اش در مدل‌سازی و تحلیل‌های مهندسی مورد استفاده قرار می‌گیرد. هر نقطه در این فضا می‌تواند به سه جهت (X، Y، و Z) حرکت کند و حول هر کدام از این سه محور هم بچرخد. بنابراین ، یک نقطه قادر است ۶ نوع حرکت داشته باشد: سه تا حرکت انتقالی (طولی) و سه تا چرخش.

سیستم مختصات استوانه‌ای (Cylindrical Coordinate System) :
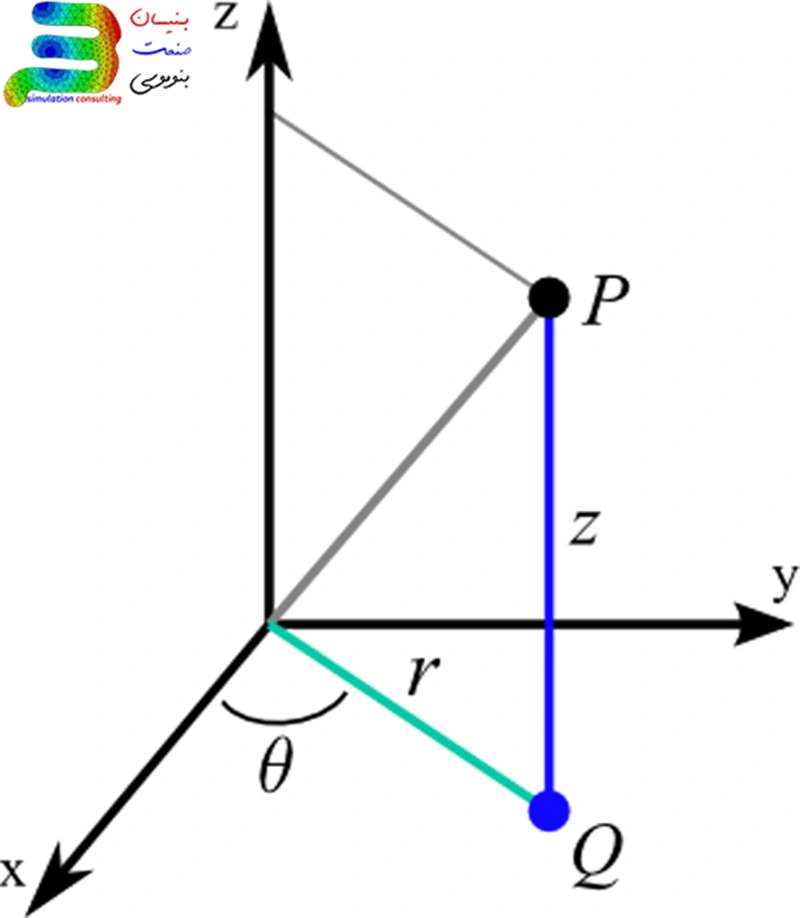
این سیستم مختصات تحلیل اجزا محدود برای مدل‌هایی مناسب است که شکل استوانه‌ای دارند یا شبیه استوانه هستند، مثل لوله‌ها، شفت‌ها، مخازن و سیلندرها. در این سیستم به جای X و Y، از R (شعاع)، θ (زاویه محیطی)، و Z (ارتفاع) استفاده می‌ شود. در این سیستم، یک نقطه می‌تواند به صورت محوری در امتداد Z و به صورت شعاعی در امتداد R حرکت کند، و  همچنین میتواند به صورت محیطی حول محور Z بچرخد. این سیستم به ویژه زمانی کاربرد دارد که بخواهیم شرایط مرزی یا بارهایی را روی مدل‌هایی که شکلی مثل سیلندر یا لوله دارند، تعریف کنیم. مثلاً در تحلیل تنش لوله‌ها یا فشار داخلی مخازن.

سیستم مختصات کروی (Spherical Coordinate System) :
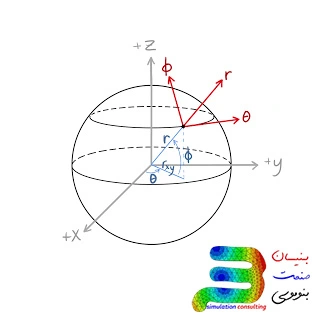
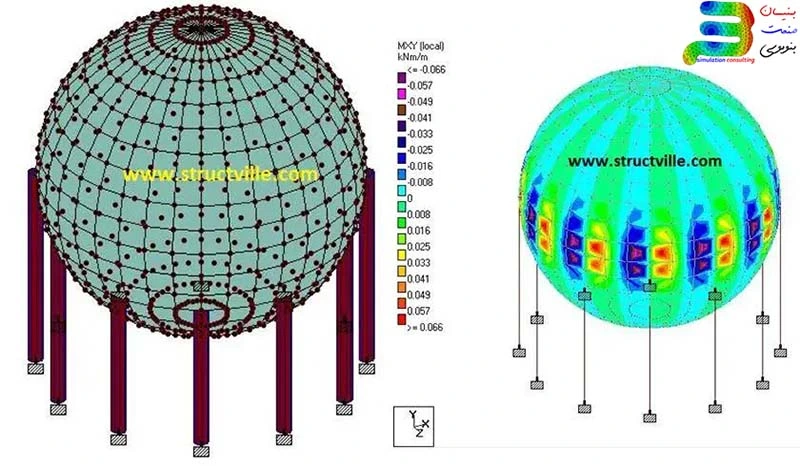
این سیستم مختصات تحلیل اجزا محدود برای مدل‌هایی که شکلی کروی دارند، مانند کره‌ها یا بعضی از گنبدها استفاده می‌شود. در این سیستم ، مختصات به صورت  r (فاصله شعاعی از مرکز)، θ (زاویه افقی)، و φ (زاویه عمودی)  تعریف می‌شود. اگرچه این سیستم کمتر در تحلیل‌های المان محدود(FEA) مورد استفاده قرار می‌گیرد ، اما برای مدل‌سازی اجسام کروی یا بررسی مسائل خاصی مانند میدان‌های الکترومغناطیسی، کاربرد دارد.

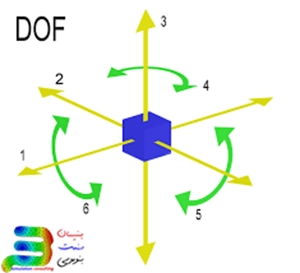
درجه‌های آزادی (Degrees of Freedom – DOF) : در تحلیل المان محدود، مفهوم درجه‌های آزادی (DOF) بسیار حائز اهمیت است. هر درجه آزادی به یکی از حرکات یا چرخش‌های یک نقطه در  فضا اشاره دارد. به طور مثال ،  در سیستم مختصات دکارتی، یک  نقطه می‌تواند سه درجه آزادی انتقالی داشته باشد(حرکت در راستای X، Y، و Z) و سه درجه آزادی چرخشی (چرخش حول محورهای X، Y، و Z)داشته باشد . این درجات ازادی معمولاً به صورت DOF 1 تا DOF 6 شماره‌گذاری می‌ شوند.

برای سیستم مختصات استوانه‌ای، درجات آزادی به صورت زیر تعریف می شوند:

• DOF 1: حرکت محوری در امتداد Z
• DOF 2: حرکت شعاعی در امتداد R
• DOF 3: چرخش محیطی حول محور θ

بنابراین ، اگر یک نقطه‌ای را در سیستم استوانه‌ای محدود کنیم تا فقط در زاویه θ بچرخد، باید درجات آزادی محوری و شعاعی (Z و R) را محدود کنیم.

تبدیل بین سیستم‌های مختصات:

گاهی لازم هست نتایج یا ورودی‌ها را بین سیستم‌های مختصات مختلف تبدیل کنیم. به عنوان مثال، اگر مدلی را در سیستم مختصات استوانه‌ای تحلیل کرده ایم، ممکن است  بخواهیم نتایج را در سیستم مختصات دکارتی بررسی کنیم. برای این منظور، باید تبدیل‌های ریاضی را انجام بدهیم:

برای تبدیل از مختصات استوانه‌ای به دکارتی:

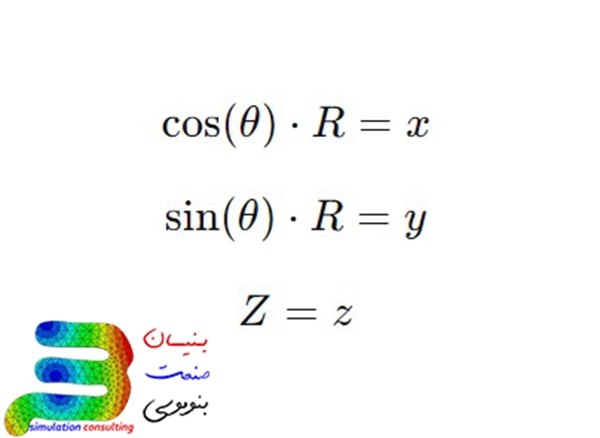
برای تبدیل از مختصات دکارتی به استوانه‌ای:

این تبدیل‌ها ضروری  هستند زیرا به ما این امکان را می‌دهند که نتایج را از زوایای مختلف بررسی کنیم و درک بهتری نسبت به رفتار سیستم به دست اوریم.

کاربرد سیستم مختصات تحلیل اجزا محدود

استفاده از سیستم مختصات تحلیل اجزا محدود به مهندس‌ها و تحلیل‌گرها این امکان را می‌دهد که شرایط بارگذاری و مرزی را به صورت دقیق‌تری مدل‌سازی کنند. به عنوان مثال ، برای مدل‌سازی یک پل فولادی، سیستم دکارتی مناسب‌تر است، اما برای تحلیل یک لوله نفتی با فشار داخلی بالا ، سیستم استوانه‌ای یا برای مخازن سیستم کروی مفیدتر خواهد بود.

تعریف شرایط مرزی و بارگذاری‌ها :

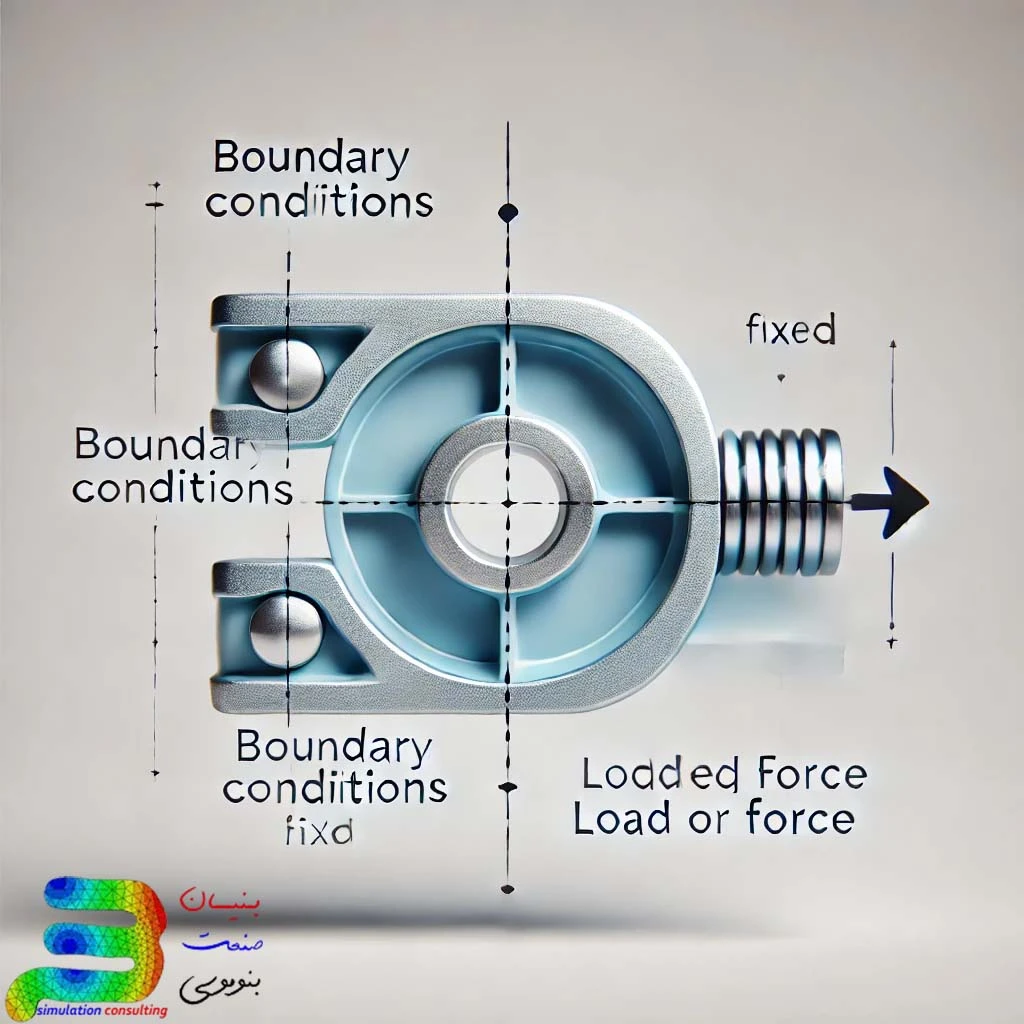
سیستم مختصات تحلیل اجزا محدود کمک می‌کنند که شرایط مرزی و بارگذاری‌ها را به طور دقیق‌تری تعریف کنیم. به عنوان مثال، هنگام استفاده از سیستم استوانه‌ای برای مدل‌سازی یک لوله، می‌توان فشار داخلی را به راحتی به صورت نیروی شعاعی تعریف کرد، و شرایط مرزی را به صورت محدودیت‌های محوری و محیطی تنظیم نمود.

شرایط مرزی در شبیه‌سازی به محدودیت‌هایی اشاره دارد که حرکت یا چرخش جسم را محدود می‌کنند، مثلاً قفل کردن یک نقطه یا لبه. بارگذاری نیز نیرویی است که به جسم وارد می‌شود، مانند فشار یا وزن. این شرایط و بارها رفتار جسم را تحت تاثیر قرار می‌دهند.

نتیجه گیری

سیستم مختصات تحلیل اجزا محدود (fea) به ما این امکان را می دهند که مدل‌ها را به دقت بیشتری شبیه‌سازی کنیم. سیستم دکارتی برای اکثر سازه‌ها کاربردی تر است ، سیستم  استوانه‌ای برای مدل‌های لوله‌ای و استوانه‌ای مناسب است، و کروی هم برای شکل‌های خاصی مثل کره‌ها به کار می‌رود. درجه‌های آزادی نیز برای تعریف محدودیت‌ها و حرکات بسیار مهم هستند. امیدوارم این توضیحات به شما کمک کند که به درک بهتری از مفاهیم سیستم مختصات تحلیل اجزا محدود برسید.

شرکت بنوموسی با ارائه جلسات منتورینگ آباکوس راهنمای شما عزیزان در جهت رفع و بهبود ایرادات فنی و مهندسی پروژه های صنعتی و دانشجوی تان در زمینه مدل‌سازی، تحلیل، و صحت‌سنجی نتایج می باشد. این جلسات به صورت آنلاین و حضوری برگزار می‌شود و نیم ساعت اول رایگان است. برای اطلاعات بیشتر و رزرو وقت، از صفحه منتورینگ اباکوس ما دیدن کنید.

برای کسب اطلاعات بیشتر و دریافت مشاوره رایگان، لطفاً با ما تماس بگیرید یا از وب‌سایت Banumusagr بازدید کنید. تیم ما آماده است تا شما را در دستیابی به نتایج مطلوب در تحلیل‌های عددی و شبیه‌سازی‌های مهندسی یاری کند.

راه های ارتباطی با شرکت بنوموسی :

TELEGRAM : https://t.me/BanuMusaGr

ایمیل: info@BanuMusaGr.com

تلفن همراه:  388 20 55 0915

تلفن:  35424520– 51 (98+)

آدرس: مشهد – کیلومتر 12 بزرگراه آسیایی (جاده قوچان)- جاده شهرک صنعتی توس- شهرک فناوری صنایع غذایی و بیوتکنولوژی شمال شرق- معاونت صنایع کوچک- مرکز خدمات.